More on reaction times
I previously replicated some simulations from a journal article by Ratcliff (1993) 1. These sims demonstrate that transformations such as taking inverse RTs typically improve power to detect RT differences across conditions. The problem is that the mean alone is a poor estimate of the central tendency of the underlying RT distribution, particularly in the presence of outliers - see the previous post for details.
I’ve started seeing people refer to skewed RT distributions in articles quite frequently, often as justification for performing some non-parametric test or other on reaction time differences. However, more often than not, this seems to be driven by a misunderstanding. The reasoning I typically see is along the following lines:
- Reaction time distributions are skewed.
- Parametric statistics require normal distributions.
- I must therefore use a non-parametric test to analyse reaction time differences across conditions.
I see the intent, but this argument is off, at least when comparing RTs across conditions in a repeated-measures context. The problem here is that this is one step too late. The tests are not being conducted on reaction time distributions, but on the differences between distributions of mean reaction times. Thus, skewed underlying RT distributions are no reason to switch to a non-parametric test, because the tests being conducted do not compare skewed RT distributions. There may be other reasons to switch, but this is not one.
Simulations
I used some code from my previous post to generate ex-Gaussian distributions - see my previous post for details. I’ll generate two RT distributions for a bunch of subjects - let’s say one is RTs to faces, one is RTs to non-face objects.
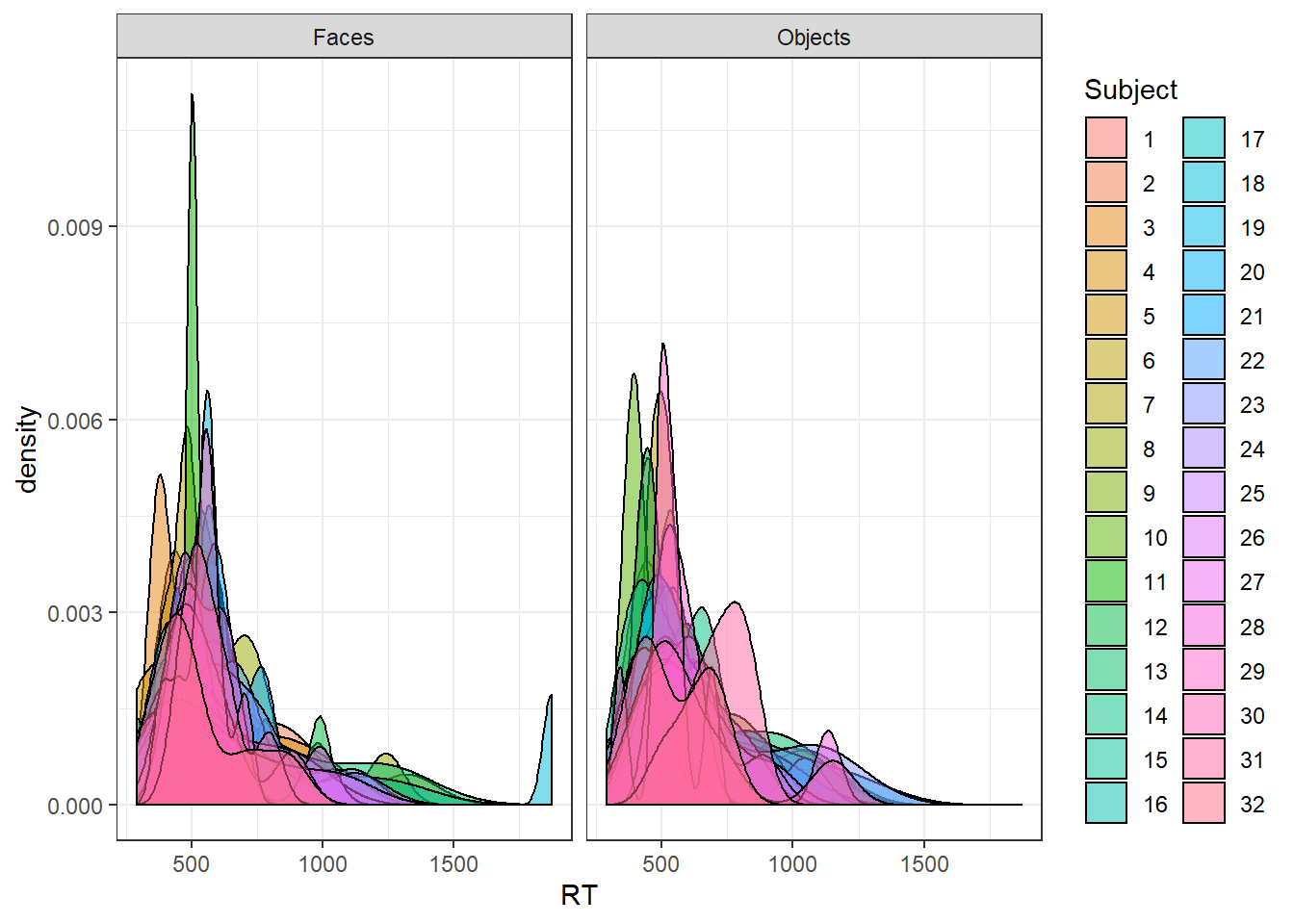
For this post, I’ll cut down the different summary statistics to four - the mean, the median, the mean of the inverse transformed RT, and the mean of log RT.
T-test versus Wilcoxon signed-rank test
I generated data from 32 subjects with a 30ms difference between conditions, 7 trials per condition, with no outliers. I did this 10000 times, and test the difference between conditions using paired t-tests and paired Wilcoxon signed-rank tests 2.
As expected, the inverse transformation comes out on top, with the mean lagging way behind. But clearly switching to the non-parametric Wilcoxon signed-rank test achieves little but a slight loss of statistical power.
“WHAT ABOUT WHEN THERE ARE OUTLIERS?!?” I hear you cry! So let’s run the simulations again, but this time with 10% of the RTs replaced with outliers.
Here, as before, power mostly drops, but worst of all for the mean. It’s clear that using Wilcoxon signed-rank tests here also achieves little. There’s a minor increase in power using WSR for tests of the median, but it’s quite a bit smaller than the shift from using the mean to using the median, and a lot smaller than the shift to using the inverse transformation. The presence of outliers in the RT distribution does not seem to matter much in terms of which test should be used, since the outliers are in the RT distribution, not in the distribution of mean RTs.
And how about when there’s no effect?
Type-I error rate is bumbling around at .05, just as we’d expect.
So why doesn’t using a non-parametric test make a difference?
There are several reasons why it doesn’t really make a difference here. The first is that even though the RT distribution is skewed, this does not mean that the distribution of mean RTs across people will be. Suppose I had a skewed distribution of 10k data points. I draw 50 points from that distribution, take the mean, then repeat 50 times. The distribution of means may well be almost normal! It may exhibit some skew, but that depends on things such as how skewed the underlying distribution is, how many observations there are, and how many participants there are.
The second is in part due to some of the underlying parameters of the simulations. Here we are comparing paired distributions within subjects. So it is not even the distribution of mean RTs that is key; it is the distribution of the differences between means. And that will also tend to be approximately normal. Note that even if the distribution of means were skewed, if the means from both conditions are both skewed in the same direction by the same amount, chances are the skew will cancel out in the differences. So, on the other hand, it’s possible that if the skew across conditions is mismatched, the differences will be skewed, and then perhaps the non-parametric test will win out. Some of these possibilities may be addressed with future simulations.
Think about how you’re summarising the data!
The message here is, if you’re concerned about the skew of RT distributions and the presence of outliers in those distributions, use a transformation before summarising the data, or use some other estimator than the mean to summarise the distribution. Don’t switch to a non-parametric test for the sake of it, or perform the transformation on the mean RTs, as that doesn’t necessarily achieve anything! I’m not saying never do non-parametric tests, or stick with doing paired t-test comparisons of the means etc.; the loss of power observed here from using non-parametric tests is minimal (and there was even a very small increase when testing differences based on median RTs), and they may well perform better when the t-test assumptions are violated. But do not swap one poor rule of thumb for another; think about why you are switching to non-parametric tests and whether they are actually necessary.
Note that there are a bunch of other reasons not to use the mean, and to use other approaches to analysing reaction time differences - see a series of posts by Guillaume Rousselet, which I recommend investigating.
Ratcliff, R. (1993). Methods for dealing with reaction time outliers. Psychological Bulletin, 114(3), 510-532 doi:↩
I also tried this out with Yuen’s d, a robust statistic based on trimmed means, and a sign test; both had consistently worse power than the t-test or the WSR (sign test was by far the worst).↩