What is intertrial coherence?
Intertrial coherence (ITC) is a measure of how consistent oscillatory phase is across an ensemble of trials.
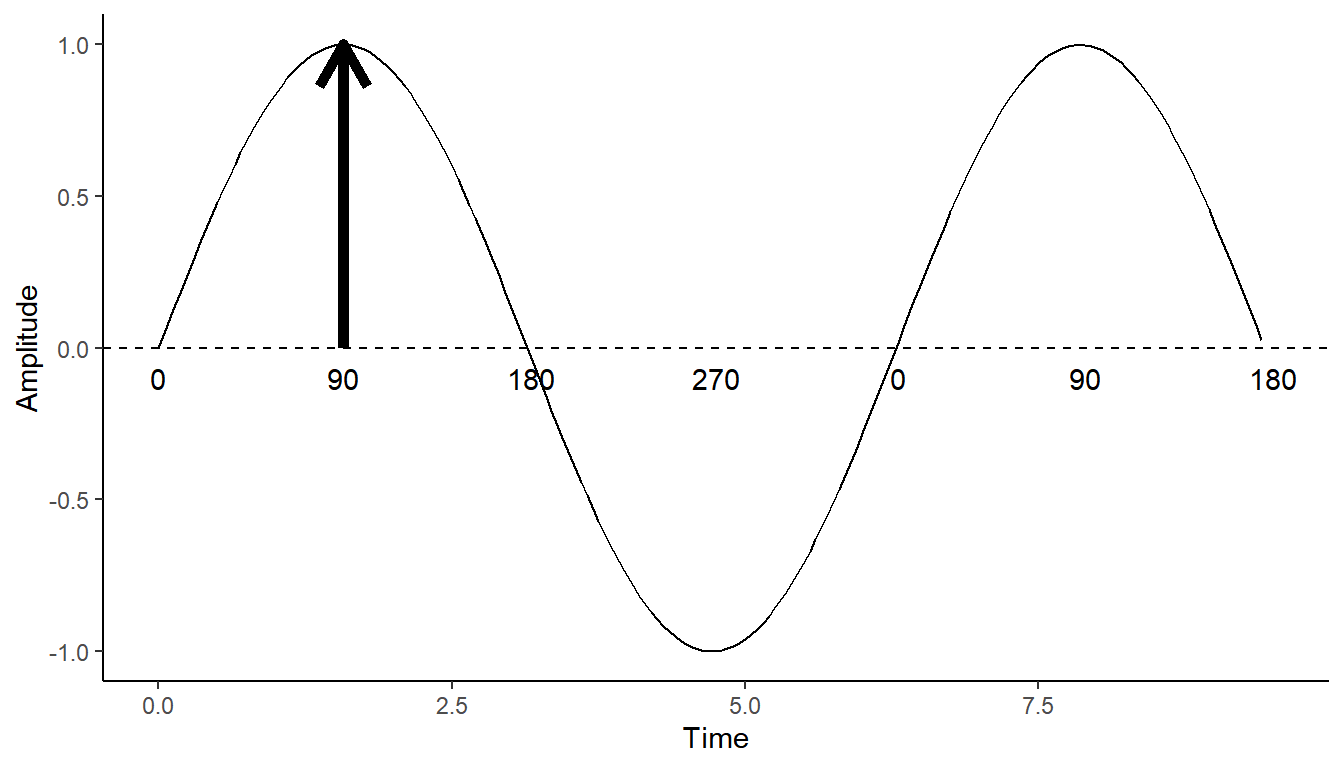
In the schematic below, we have a sine wave of an arbitrary frequency.
The amplitude of the wave is the distance between 0 and the wave at a given timepoint. So here, you can see it has a maximum of 1, indicated by the arrow. A complete cycle of of the wave is the amplitude peaking, declining to a trough, then hitting zero again. So the wave cycles from 0 up to 1, down to -1, then back up to 0.
The phase of the wave is a measure of how far through an oscillatory cycle the wave is. In the schematic below, I express that using degrees. Starting at 0, we peak at 90 degrees, hit zero again on the way down at 180 degrees, trough at 270 degrees, then return to 0 at 360 degrees, where we begin the cycle again.
A question we might have when examining oscillations in EEG or MEG data is how consistently they reach the same point in the cycle across trials. That’s where intertrial coherence comes in!
The maths behind intertrial coherence
When we perform time-frequency analysis, we are performing a moving window Fast Fourier Transform. The FFT returns Fourier coefficients for each combination of time and frequency - complex numbers with real and imaginary components that describe a position in a two-dimensional plane. These complex numbers represent both the magnitude and the phase of the signal.
A fantastic visualization by Natalie Schaworonkow demonstrates the principle of intertrial coherence. On the x-axis we have time, on the y-axis we have trial number. When the oscillation reaches the same phase at the same time on each trial, we have high ITC. As the phase gets more and more misaligned across trials, ITC decreases.
Inter-trial coherence measures phase-synchronization across trials. It is the circular sum of phases at a certain point in time (length of red arrow). It reaches its maximum value of 1 for perfectly phase-aligned signals and becomes 0 as the phase distribution becomes uniform. pic.twitter.com/jv2unSVC7O
— Natalie Schaworonkow (@nschawor) December 17, 2019
ITC is bounded between 0 and 1, with 1 being perfect intertrial coherence (i.e. exactly the same phase on every trial), and 0 being absolutely no intertrial coherence. With a real signal, you’ll only see 0 or 1 if you’ve done something wrong!
ITC can be calculated as follows.
Step-by-step, we begin with the Fourier coefficients derived using the FFT: \[Z_i(f)\]
We divide the Fourier coefficients by their absolute values: \[\frac{Z_i(f)}{\left| Z_i(f) \right|}\]
This normalises the values to be on the unit circle.
The next step is to take the mean of these values:
\[\frac{1}{n} \sum{^n_{i = 1}} \frac{Z_i(f)}{\left| Z_i(f) \right|}\]
Finally, we take the absolute value of the complex mean. This leaves us with the ITC:
\[ ITC(f) = \left| \frac{1}{n} \sum{^n_{i = 1}} \frac{Z_i(f)}{\left| Z_i(f) \right|} \right|\]
Let’s see this process in action on some real data.
Calculating ITC
To be able to calculate ITC, we’re going to need the Fourier coefficients for every single trial.
demo_tfr <- compute_tfr(demo_epochs,
foi = c(4, 30),
n_freq = 27,
n_cycles = 3,
keep_trials = TRUE,
output = "fourier")## Output frequencies: 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30## Removing channel means per epoch...Let’s have a look at raw power at all of the electrodes. Fourier coefficients can be converted to power by taking their absolute values and squaring them. plot_tfr() does that for us automatically.
plot_tfr(demo_tfr) +
facet_wrap(~electrode)## Data is complex Fourier coefficients, converting to power.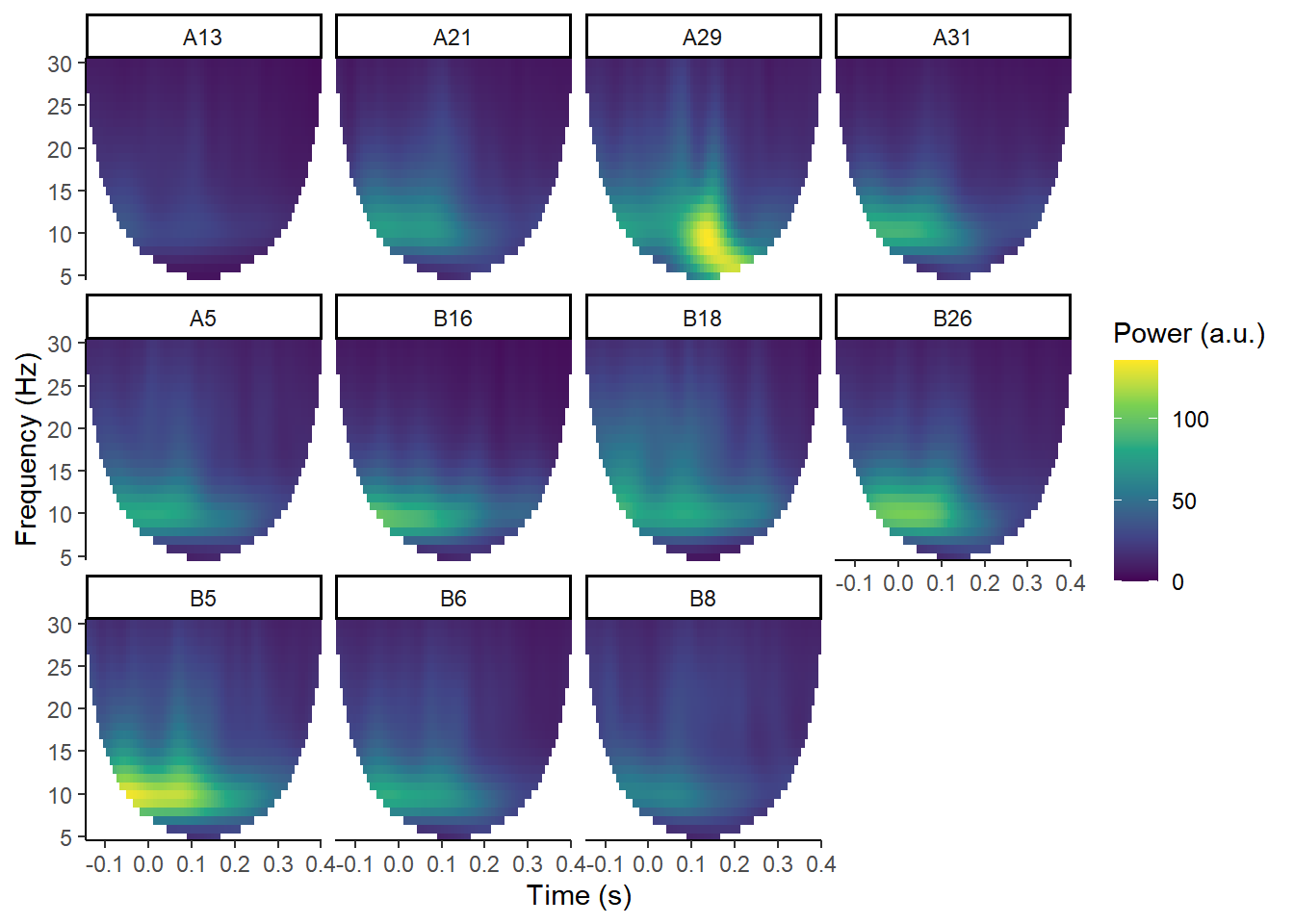
These plots show total power at the 11 electrodes in this data.
Ignore all the white at the edges; that’s just where the edges have been removed to avoid edge effects from the convolution process. This data is a bit short for demoing TFRs, but it’ll do for our purposes. You should be able to pick out that at A29 (roughly, Oz), there’s a post-stimulus power peak. That corresponds to the timing of a visual ERP.
Instead of taking the steps above, let’s convert our Fourier coefficients to phase angles. When we convert to phase angles, we set the magnitude to 1, placing phase on the unit circle. We can draw a polar plot, showing the position of each of the phase angles on that circle.
Let’s pick a single time point from the A29 electrode. I’ll pick out the Fourier coefficients from one timepoint, approximately 178 ms after stimulus onset, at 10 Hz.
demo_tfr$timings$time[49]## [1] 0.1777344all_fourier <- demo_tfr$signals[, 49, 4, 7]
phase_angle <- Arg(all_fourier)
circ.plot(phase_angle)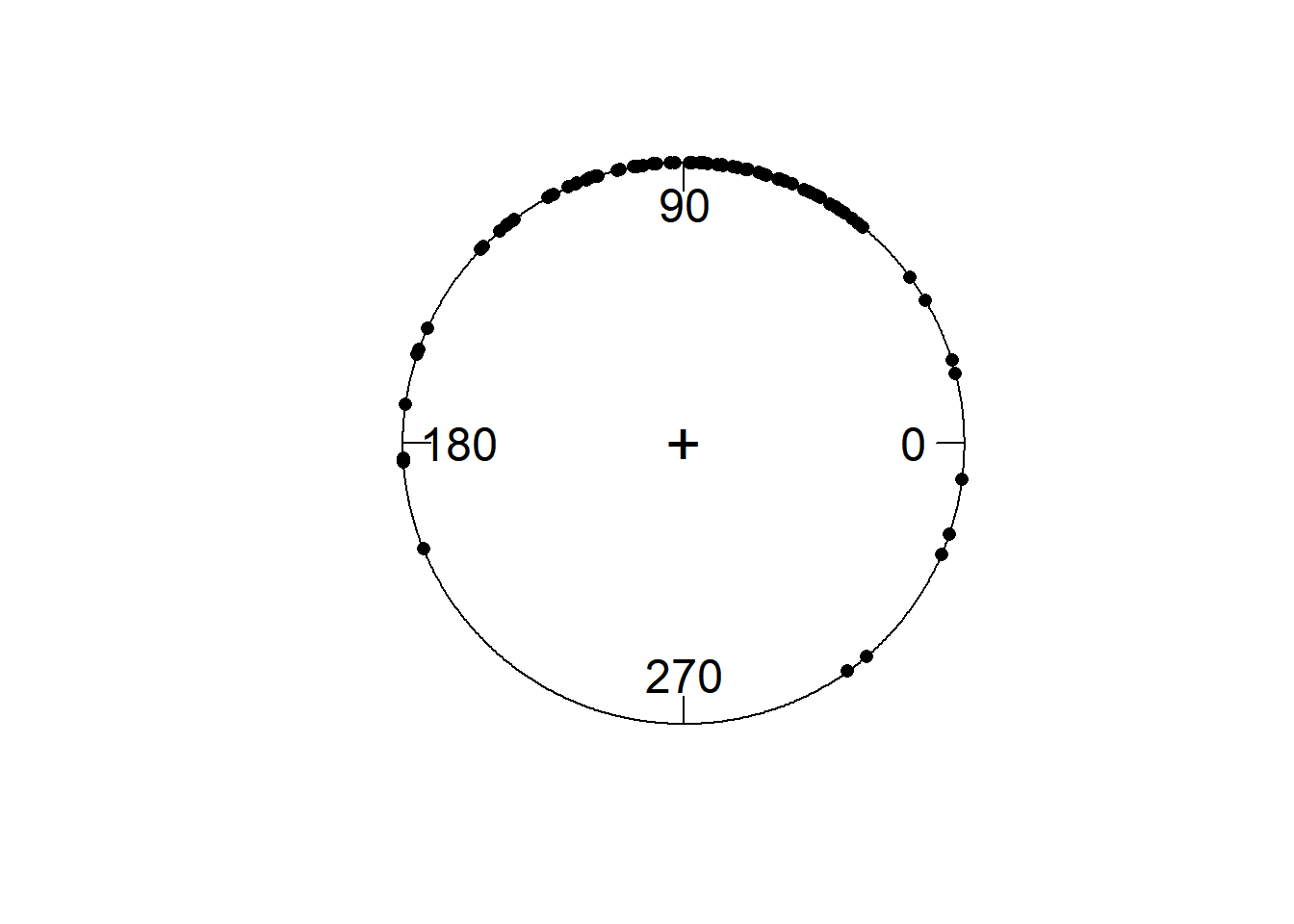
Each dot represents phase at a single time-point on a single trial.
ITC is a measure of how much those points cluster together. Something apparent from this plot is that there are many more phase angles around 90 degrees then there are around 270. If we wanted to know the average phase angle, we’d have to calculate the circular mean. Unlike amplitude, phase is a circular variable, just like time, or the degrees on a compass. Thus, 360 degrees and 0 degrees are the same; 359 degrees and 1 degree are 2 degrees apart, not 358 degrees.
circ.mean(phase_angle)## [1] 1.56209Note this is in radians rather than degrees.
But for ITC, the phase angles themselves are not so relevant. What matters is how dispersed they are around the circle.
Converting to ITC
Let’s convert the formula above to R code and calculate ITC at our single representative timepoint:
abs(sum(all_fourier / abs(all_fourier)) / length(all_fourier))## [1] 0.7334559We have an ITC of ~.73! That’s pretty high.
Now, with a few more lines of code, I’ll convert all the data to inter-trial coherence, and plot ITC at A29.
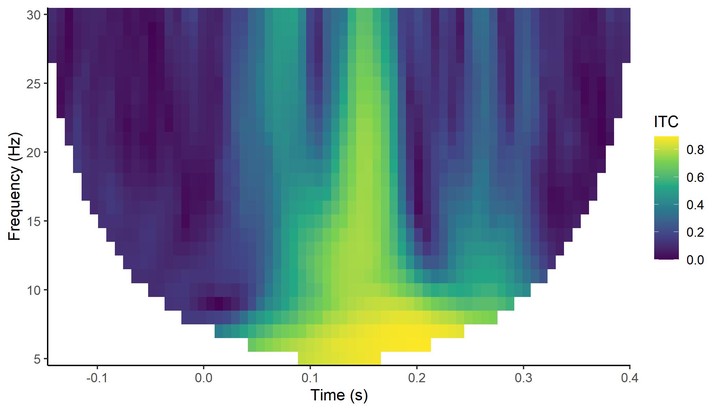
demo_ITC <- compute_ITC(demo_tfr)
plot_tfr(demo_ITC, electrode = "A29") +
labs(fill = "ITC")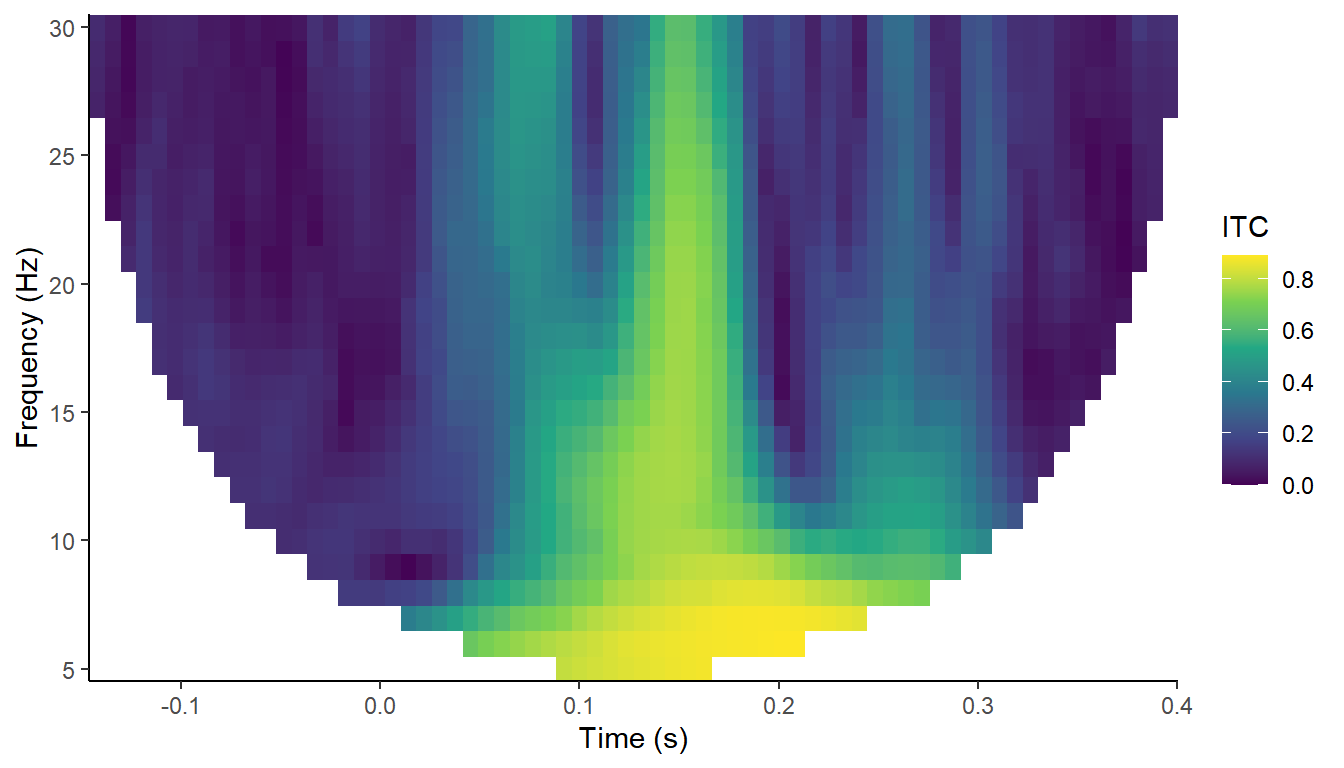
From this we can see the phase of the oscillations recorded at A29 seems to align much more strongly across trials at around 150-180 ms, across most frequencies. This is approximately the time at which the ERPs to visual stimuli are peaking.
plot_timecourse(demo_epochs,
"A29",
baseline = c(-.1, 0))## Joining, by = c("epoch", "recording", "epoch_label", "participant_id")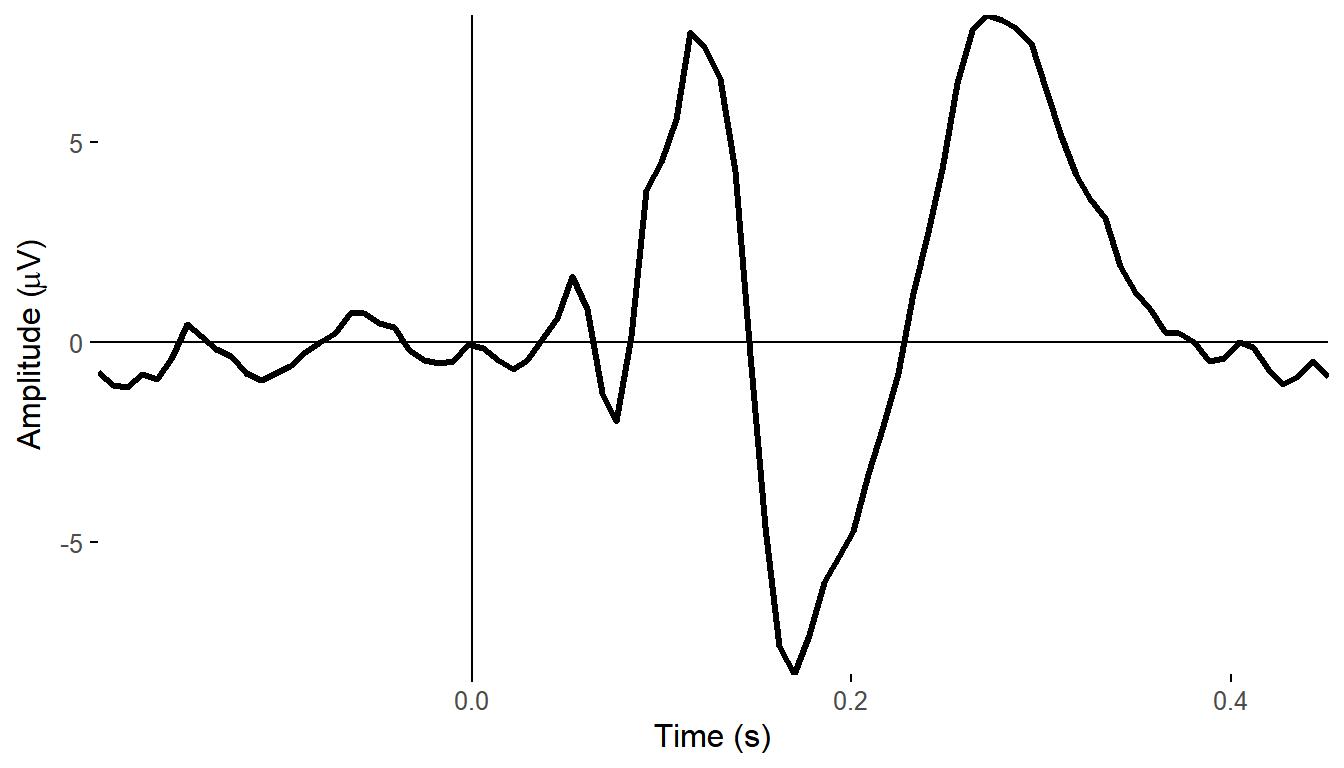
Thus, one interpretation of ITC is that it is capturing what we’d call evoked power - the power of the ERP - (left panel below) as opposed to induced or total power (right panel below). It is teasing out the phase-locked as opposed to non-phase-locked activity.
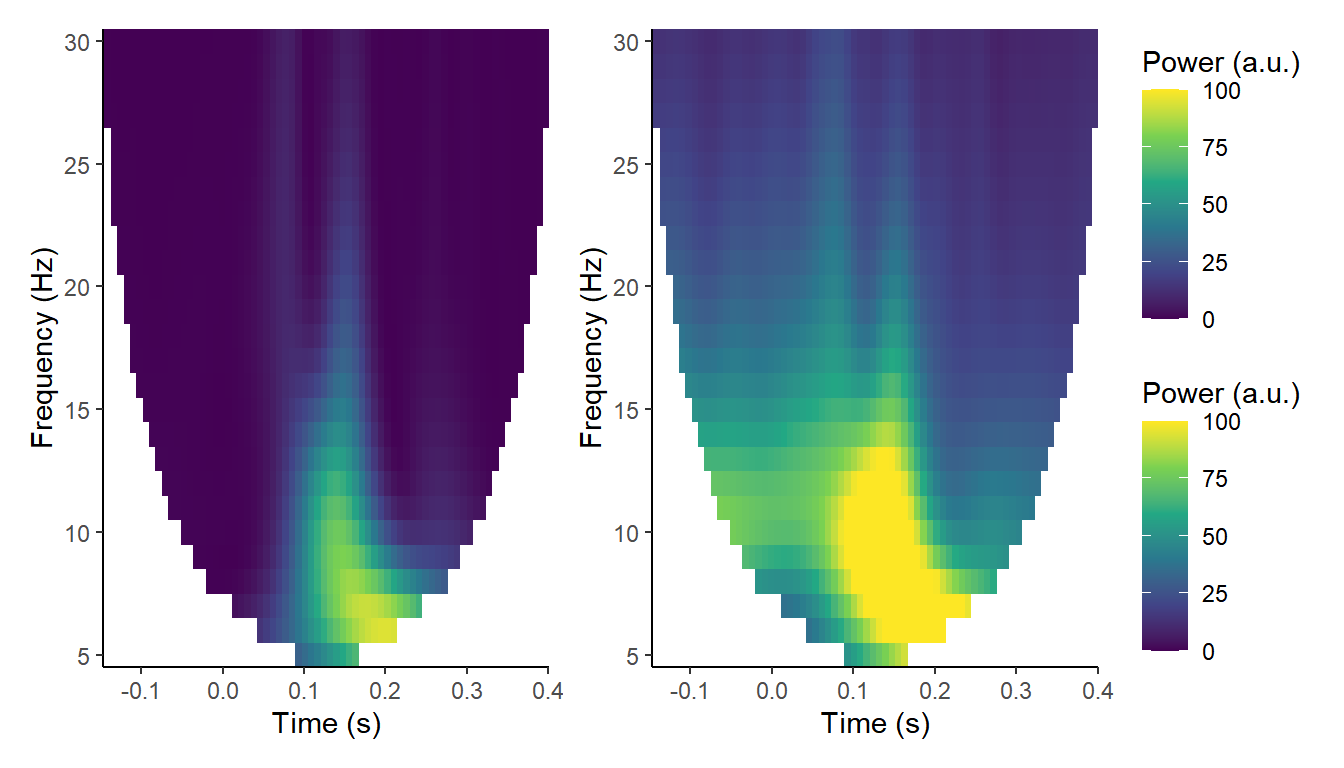
One thing to bear in mind is that ITC is a compound measure, a summary statistic that doesn’t in and of itself exist on a single-trial level. There have been several articles recently attempting to overcome this using a technique called jackknifing to relate it to single-trial behavioural measures such as reaction times. I’ll be looking at that in another post.